[3.1]

         (3.1a)

         (3.1b)

平衡点を(x₀,y₀) ;(x₀,y₀>0)とすると、

       (3.1’a)

      (3.1’b)

x₀,y₀>0より、x₀=c/b, y₀=r/a。

平衡点からのずれ(n₁,n₂)=(x-x₀,y-y₀)を用いて、(x,y)=(x₀+n₁, y₀+n₂)によって、(3.1a)式は

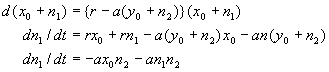
(3.1b)式は

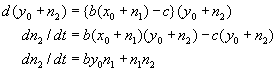
ここで、n₁,n₂は十分に小さいので二次の項は無視できる。

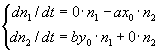
従って、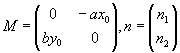　と書くと、上式はdn/dt=Mn と書ける。

このときの固有値λは、　を満たすので、

　

となり、λは純虚数となる。また、(2.10)式と(2.12)式より上で求めたλをに当てはめると、

　

このとき、周期は なので、 となる。

 

[3.2]

§3.6を参照のこと。

Kが無限大なので、

           (3.3’a)

           (3.3’b)

V(x,y)を時間微分して、

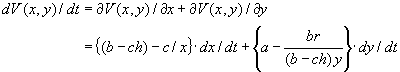
(3.3’)式を代入して整理すると、

r,h,b-ch>0 なので、dV/dt≧0。

 

[3.3]

(3.3)式

            (3.3a)

                         (3.3b)

ただし、b-ch>0．

 

(1) 求める平衡点の座標を(x,y)= (x₀,y₀) ;(x₀,y₀>0)とおくと、

                 …�@

                                …�A

�A式よりy₀≠0なのでx₀について整理して、x₀=c/(b-ch)

�@式よりx₀≠0なのでy₀について整理して、y₀=(r/a)(1- x₀/K)(1+h x₀)

 

(2) 演習3.1を参照。

平衡点からのずれ(n₁,n₂)=(x-x₀,y-y₀)を用いて、(x,y)=(x₀+n₁, y₀+n₂)によって、(3.3)式は

(3.1b)式は

ここで、n₁,n₂は十分に小さいので二次の項は無視でき、

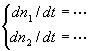
従って、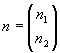　と書くと、上式はdn/dt=Mn と書けるので、平衡点(x,y)=(x₀,y₀)における線形化力学系の行列の要素は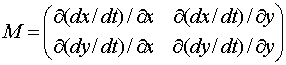　となる

 

(3) 固有値λが従う方程式は

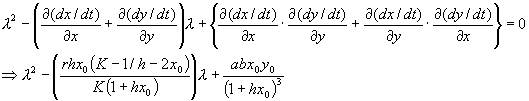
λが複素数根を持つとき、なので（→2.13式を参照）、λの実部αはと表せる。

r,h,x₀,K>0 なので、αの正負の判別はで行えばよい。つまり平衡点は、

 ならα<0なので安定。               …（＊）

 ならα>0なので不安定。           …（＊＊）

となる。

 

(4) dx/dt=0のアイソクラインは　　なのでxについて整理して、

　

となり、上に凸の放物線である。このとき、この放物線の頂点のx座標は となる。

一方、dy/dt=0のアイソクラインは。この2本のアイソクラインの交点が共存平衡点である。

よって、平衡点がdx/dt=0のアイソクラインの頂点より左（つまり、）にあるとき、。

これは(3)の安定性の解析（＊＊）と同義で、平衡点は不安定となる。

　逆に平衡点がdx/dt=0のアイソクラインの頂点より右にある場合は(3)の安定性の解析（＊）と同義で、平衡点は安定となる。

 

 

[3.3]

　ロトカ･ボルテラ競争系の(2.1)式では、原点でない平衡点(x₀,y₀)は、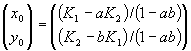で、この(x₀,y₀)を用いて(2.1)式を変形すると、

                …(2.1’a)

               …(2.1’b)

与えられたV(x,y)を時間微分して、

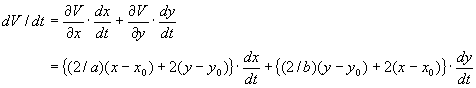
(2.1’)式をそれぞれ代入して整理すると、

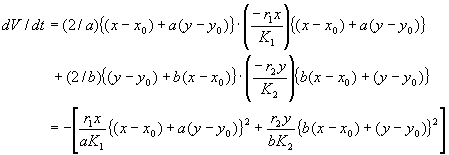
a,b,r,K,x,y>0なので、dV/dt≦0。ただし等号の成立は(x,y)= (x₀,y₀)のとき。